Первый тип задач по теории вероятности.
а) задачи на симметричную монету (если бросают 3 и более раз).
В случайном эксперименте симметричную монету бросают 4 раза. Найти вероятность того, что орел не выпадет ни разу.

б) если бросают дважды
Симметричную монету бросают дважды. Найти вероятность того, что решка выпадет 2 раза.
О – орел
Р – решка
Найдем все исходы:
ОО
ОР
РО
РР
P (вероятность) = 1/4 = 0,25
Второй тип задач по теории вероятности.
Задачи на игральные кости.
В случайном эксперименте бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет не менее 10 очков (округлить до десятых).
P = K/N
Если бросают 1 раз, то N = 6
Если бросают 2 раза, то N = 6^2= 36
Если бросают 3 раза, то N = 6^3 = 216
Решение:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
P = 6/36 = 1/6 ≈ 0,2
Третий тип задач по теории вероятности.
Фиксированные события и элементы.
Фиксированные события сводятся к классическим задачам на вероятность, достаточно уменьшить число n или k, или только n, или только k на 1.
Пример:
В классе 21 ученик. Есть 2 друга: Максим и Петр. Класс разбивают на 3 равные группы. Найти вероятность того, что они окажутся в одной группе.
| I группа | II группа | III группа |
| 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 | 1 2 3 4 5 6 7 |
N = 20
K = 6
P = K/N = 6/20 = 0,3
Четвертый тип задач по теории вероятности.
Несовместимые события.
Такие события, которые не могут происходить одновременно.
| P (A + B) = P (A) + P (B) |
Несовместимые события – это такие события, где вероятность одного не зависит от другого.
Союз «или» => сложение.
| P = (A × B) = P(A) × P(B) |
Союз «и» => умножение.
Пример:
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
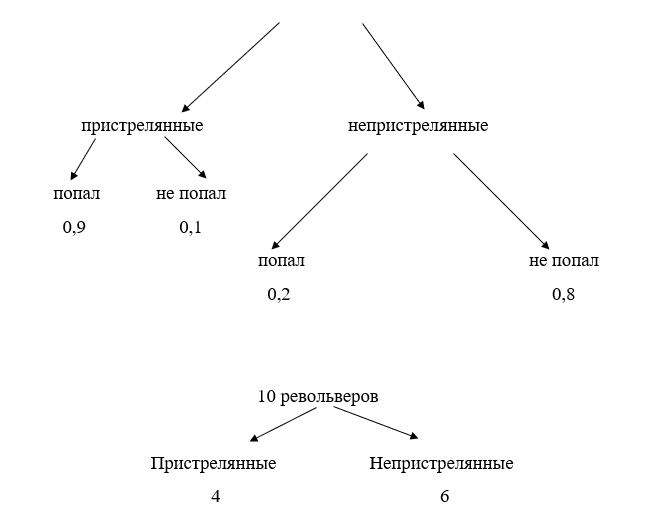
Решение:
P = 0,1 × 0,4 + 0,8 × 0,6 = 0,52
Пятый тип задач по теории вероятности.
Футбольный матч.
Пример:
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.
Решение.
В – жребий выпадет
П – жребий не выпадет
| ВВВ | ВПП |
| ВВП | ППВ |
| ВПВ | ПВП |
| ПВВ | ППП |
P = K/N
P = 3/8 = 0,375
Шестой тип задач по теории вероятности.
«Кофе-автомат».
Пример:
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится в обоих автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
О – осталось
З – закончилось

0,35 – 0,16 = 0,19
Р – 1 – 0,19 – 0,19 — 0,16 = 0,46.
Седьмой тип задач по теории вероятности.
Вероятностные диапазоны.
Пример:
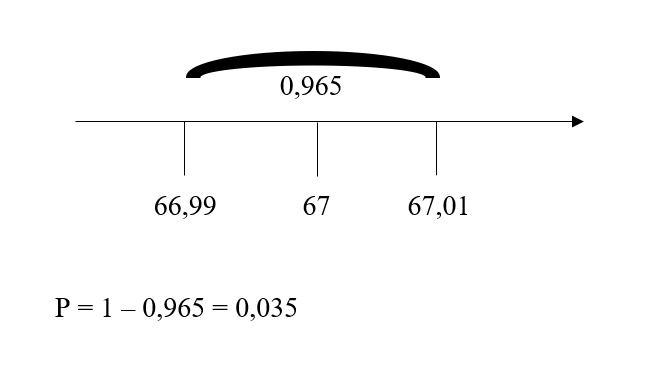
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0.01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 66,99 мм или больше, чем 67,01 мм.
Решение: