Задание №5 — задания на сложную вероятность

В задании 5 акцент чаще всего делается на более сложные задачи, требующие использования нескольких подходов для их решения. Этапы решения могут включать:
Формулировка проблемы
Здесь также важно четко понять, что именно требуется — оценить вероятность определенного события, найти условную вероятность или рассмотреть несколько событий одновременно.
Характеристика случайных событий
При необходимости определите, являются ли события независимыми или зависимыми, совместными или несовместными. Это определит выбор методики расчетов.
Использование формул
При решении задач, в зависимости от типа и сложности событий, могут понадобиться различные формулы. Например, для условной вероятности P(A|B) будет использоваться формула P(A|B) = P(A и B) / P(B).
Комбинации и перестановки
Для некоторых задач может быть необходимо применять комбинаторные методы. Например, для нахождения количества благоприятных исходов в задачах на выбор можно использовать формулы для вычисления сочетаний и перестановок.
Симуляция и моделирование
В некоторых случаях можно воспользоваться методами симуляции, чтобы получить приближенные значения вероятности, особенно если аналитическое решение кажется трудным.
Проверка и анализ ответа
Как и в предыдущем задании, важно проверить полученное значение на логичность и соответствие условию задачи., где К – число благоприятных исходов;
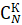
=